1	El número es la esencia de todas las cosas. Pitágoras. Dios geometriza el mundo por eso el lenguaje matemático es imprescindible para descifrar sus secretos. Galileo.

GUÍA DEL PROFESOR

TEMA: ¿Qué son las matemáticas?
Resultados esperados
Al término de la sesión los estudiantes:
Reconocerán que las matemáticas esenciales están compuestas tanto por la aritmética como por la geometría.
Valorarán la importancia del pensamiento lógico matemático a través de la historia de la humanidad.

Introducción

La matemática nació como ciencia y sigue siéndolo y, por tanto, trata en sus desarrollos de develar y dominar alguna porción del mundo real, interior o exterior al hombre. Por eso no es un mero arbitrario juego lógico. Sus postulados y sus leyes de inferencia están fuertemente inspirados en una fracción de la realidad. Es de aquí de donde le viene a la matemática su complejidad y su riqueza, reflejos de la riqueza y complejidad del mundo real mismo. El misterio de la adecuación de ese mundo matemático, tan propio de la mente que ha surgido de ella y de una mirada suya al universo, con la realidad externa es algo que no ha dejado de maravillar a los científicos de todos los tiempos. Pese a todo ello podemos afirmar que existen razones poderosas para considerar el conocimiento matemático como modelo de conocimiento científico, ya que ningún otro tipo de ciencia alcanza su objetivo propio con tanta eficacia, evidencia y certeza como lo logra el método matemático.1

La antigua definición de las matemáticas como ciencia del número (lo que da origen a la aritmética) y del espacio (lo que da lugar a la geometría) al través de los siglos, ha dado lugar a la complejidad del símbolo (el álgebra), a la complejidad del cambio y la causalidad (el cálculo), la complejidad de la incertidumbre (probalidad y estadística) y la complejidad de la estructura formal del pensamiento (la lógica matemática).

Es decir que, desde que las matemáticas se conciben como tal, se ha desarrollado desde dos vertientes: la aritmética y la geometría; la primera estudia las relaciones cuantitativas y la segunda las formas espaciales, a través de diferentes procesos surgen nuevas ramas del pensamiento lógico matemático. Federico Engels planteaba que: “el objeto de las matemáticas son las relaciones cuantitativas y las formas espaciales del mundo real”.

Sugerencia didáctica: Es importante que usted explique a los estudiantes que las matemáticas en esencia son números y formas geométricas, que son todo lo que encontramos en la realidad, en nuestro entorno, por ello es fundamental que reconozca la relevancia de su estudio porque nos sirve para explorar racionalmente el espacio físico en que vivimos.

ACTIVIDAD 1

A modo de introducción antes de iniciar la siguiente lectura, explíquele a sus alumnos por qué es importante el conocimiento de la aritmética y el álgebra, la geometría, el cálculo, la estadística y la probabilidad:

La aritmética y el álgebra juegan un papel primordial en la formación de los estudios universitarios, ya que son elementos que promueven la capacidad de abstracción y generalización en los estudiantes, debido a que les permiten descubrir un lenguaje simbólico con el cual pueden representar situaciones reales y modelar algunos problemas.

La geometría les permite una abstracción de la realidad que no sólo se basa en sus estructuras cognitivas lógicas, sino también en sus estructuras relacionadas con la imaginación espacial. Es la rama de las matemáticas más adecuada para introducir a los estudiantes al razonamiento deductivo; se desarrolla al proponer análisis de ejemplos que lleven a formar conjeturas sobre las relaciones que hay entre las diversas formas geométricas.

El cálculo le resulta provechoso para tener la idea clara de lo que es una función, lo que es un límite, una derivada y una integral. El cálculo es uno de los pináculos de las matemáticas en el nivel superior, pues se conjugan ahí los métodos algebraicos y geométricos, permitiendo que todo aquello que se estudió previamente tenga una aplicación conjunta e integral.

La estadística y la probabilidad les permiten aplicar sus conocimientos llevando a cabo cálculos con los que pueden eliminar mucho trabajo de operaciones, dedicando el tiempo al análisis y la interpretación de los resultados para comprender la situación que producen los datos, los cuales les pemiten a su vez, la resolución de problemas o tomas de decisiones fundadas en evidencias más objetivas y no sólo en criterios intuitivos y subjetivos.

La probabilidad y la estadística son componentes muy importantes en nuestra cultura y en muchas ciencias por ello deberían constituir una parte importante del bagaje cultural de los estudiantes en nuestra sociedad.

Los estudiantes leen y reflexionan sobre el siguiente texto de Pedro Miguel González Urbaneja2. Sugiérales que formen parejas de trabajo y realicen un escrito en donde manifiesten la importancia de las matemáticas (aritmética, álgebra, geometría, cálculo, probabilidad y estadística) en su comunidad; si es posible que compartan alguna experiencia muy evidente de ello. Al final expondrán el texto reflexivo al grupo.

Como herederos del mundo clásico, nosotros, profesionales
de la transmisión del conocimiento matemático, enfatizamos
con vehemencia las cualidades de las Matemáticas: la
capacidad para manejar la cantidad y la extensión, la
regularidad y la disposición, la estructura y la implicación,
la inducción y la deducción, la observación y la imaginación,
la curiosidad y la iniciativa, la lógica y la intuición, la
invención y el descubrimiento, el análisis y la síntesis, la
generalidad y la particularidad, la abstracción y la concreción,
la interpolación y la extrapolación, la decisión y la
construcción, la belleza y la utilidad, la armonía y la creatividad,
la interpretación y la descripción[...] siempre bajo la
acción del entendimiento y el imperio de la voluntad. Estas
cualidades inherentes a las Matemáticas alimentan su función
informativa: adquirir un conjunto de conocimientos
que permitan familiarizarse con el mundo natural circundante,
con herramientas para interpretar el mundo físico,
natural y social, en términos cuantitativos y abstractos,
pero sobre todo, por imperativo platónico, la función formativa:
desarrollar el pensamiento crítico y el rigor científico,
inculcar una disciplina mental con la que operar sobre
cualquier tipo de pensamiento o de situación y a través de
la resolución de problemas desarrollar la iniciativa personal
y la fortaleza para vencer obstáculos, estimulando la
voluntad. La Matemática incide así decisivamente sobre el
binomio entendimiento-voluntad que es la matriz del espíritu
humano, de ahí la implicación trascendental que como
en los tiempos de Platón tiene hoy y siempre la Matemática
en la Educación. (González, 2001b, p.15).

ACTIVIDAD 2

Esta actividad de estudio independiente tiene como objetivo sensibilizar a los alumnos con relación a la visión del pensamiento lógico matemático, para ello les pedimos que vean la película “Mente indomable”, la cual aborda el talento innato de un joven para las matemáticas y la problemática de su personalidad en su vida cotidiana.

Sugerencia didáctica: Insista a sus alumnos que observen la película con mucha atención porque con base en ella tendrán que responder las siguientes preguntas, emitir una opinión y sacar sus propias conclusiones.

Preguntas:

1.- ¿Crees que las matemáticas son fundamentales en la vida del protagonista, y por qué?

2.- ¿Te identificas con el personaje: tienes aptitudes para las matemáticas y te gustan; o por el contrario: eres opuesto a él, no las comprendes y no te gustan?

3.- ¿Qué opinas de las mentes brillantes que han desarrollado planteamientos matemáticos fundamentales a través de la historia, como el protagonista de la película y los matemáticos inmortales?

4.- Después de haber visto la película, de responder a las preguntas anteriores y el trabajo de toda esta sesión ¿qué reflexiones y aprendizaje te dejan?

1 DE GUZMÁN, Miguel (1983): Algunos aspectos insólitos de las matemáticas, artículo publicado en línea de la Revista Investigación y Ciencia. En: Revista Iberoamericana de Educación No. 42/4 – 10 de abril de 2007. Disponible en: http://carmesimatematic.webcindario.com/guzman.htm#filosofia
2 GONZÁLEZ U., Pedro Miguel. La historia de las matemáticas como recurso didáctico e instrumento para enriquecer culturalmente su enseñanza. Revista SUMA. Febrero, 2004. España. p. 26.

2	La Historia de la Matemática pone de manifiesto la dimensión cultural de las Matemáticas y su notable impacto en la Historia del Pensamiento. La perspectiva histórica permite dar una visión panóramica de los problemas matemáticos. Pedro Miguel González Urbaneja (2004).

GUÍA DEL PROFESOR

TEMA: Historia de las matemáticas.

Resultados esperados:

Al término de la sesión los estudiantes:
Conocerán el contexto histórico en el que surgieron las bases fundamentales de las matemáticas.
Conocerán algunas de las principales biografías de los más importantes matemáticos a lo largo de la historia, así como los planteamientos que los hicieron inmortales.
Introducción

Con argumentos apoyados en numerosos textos de ilustres matemáticos, pedagogos, historiadores y profesores, se reclama una función didáctica para la Historia de las Matemáticas como instrumento de comprensión de sus fundamentos y de las dificultades de sus conceptos para así responder a los retos de su aprendizaje. La Historia es fuente de inspiración, autoformación y orientación en la actividad docente y al revelar la dimensión cultural de la Matemática, el legado histórico permite enriquecer su enseñanza y su integración en el conjunto de los saberes científicos, artísticos y humanísticos que constituyen la Cultura.1

Los resultados del razonamiento lógico matemático son un producto cultural, es decir, son relativos a un contexto socio-histórico: la importancia de un teorema es algo contextual relacionado con el momento histórico en que fue desarrollado. Conocer las necesidades que motivaron en su momento la introducción de un concepto nuevo, así como las dificultades que tuvieron que ocurrir para que esos nuevos conocimientos salieran a la luz.

El conocimiento de la historia favorece la comprensión profunda de los problemas matemáticos, por medio del conocimiento del proceso real de creación de esos conceptos, en el contexto en que aparecen, de las ideas que los propician y de las cuestiones que los resuelven.

La historia de las matemáticas también es importante porque nos muestra que se ha llegado a los mismos resultados matemáticos por caminos diferentes.

Propósito:

El tutor explicará porque es importante abordar el pensamiento lógico matemático desde un enfoque histórico, es decir, que las matemáticas surgen en un contexto socio cultural determinado y que impacta a la sociedad de la época en que se desarrolla.

Introducción:

Es relevante que usted exponga a los estudiantes la importancia de contextualizar históricamente cómo surgen los razonamientos matemáticos, con base en las necesidades de la sociedad que los produce. Enfatice que los contenidos de matemáticas, como de cualquier otra ciencia, no son algo acabado, atemporal, sin relación con una época y una sociedad determinada, sino por el contrario, como una disciplina viva y relacionada con la cultura imperante.

Se debe destacar que el proceso para llegar al conocimiento o resolución de algún problema, en un primer momento fue un reto aún para los matemáticos que los resolvieron, en gran similitud con las dificultades que los estudiantes atraviesan.

ACTIVIDAD 1

Los estudiantes realizarán la lectura en voz alta a todo el grupo “Sobre la historia de las matemáticas” que viene en la sección de Competencia Pensamiento lógico-matemático en la Antología.

Compartirán con el grupo la reflexión que la lectura les sugiere. Asimismo, comentarán alguna experiencia que como estudiantes hayan escuchado sobre algún matemático famoso, cómo descubrió su teorema, en qué circunstancias desarrolló sus estudios matemáticos, cuál era el contexto histórico en el que hizo su descubrimiento e implementó su trabajo, etcétera.

Sugerencias didácticas: Con base en las lecturas complementarias que le proporcionamos al final de esta sesión o bien en otras fuentes, prepare para esta sesión alguna anécdota de algún filosófo griego que haya incursionado en la enseñanza de las matemáticas, comente sobre su obra, sus aportaciones a la sociedad en la época en que desarrolló sus teorías y conocimientos. Esta aportación será de mucha utilidad para el desarrollo de la actividad de estudio independiente de sus alumnos, ya que lo utilizarán como ejemplo.

ACTIVIDAD 2

Los estudiantes investigarán sobre la vida y obra de otros matemáticos relevantes. Con la información que recopilen sobre el que ellos elijan, elaborarán un escrito de una cuartilla de dicho personaje.

Sugerencias didácticas: Enfatíceles que es importante que incluyan la época en que ese personaje vivió, el contexto histórico, político y social en que realizó sus descubrimientos matemáticos, los motivos que lo llevaron a incursionar en el pensamiento lógico matemático y el impacto que tuvo en su entorno la implementación de sus aportes a las matemáticas y a la vida cotidiana de su época.

Lecturas complementarias que apoyarán su exposición sobre las anécdotas de los sabios matemáticos:

GONZÁLEZ U., Pedro Miguel. La historia de las matemáticas como recurso didáctico e instrumento para enriquecer culturalmente su enseñanza. Revista SUMA. Febrero, 2004. España. pp. 17-28.

Tarbiya: revista de investigación e innovación ed., núm. 15 (Enero-Abril,1997) 126 pag.

KLINE, M. (1992): El pensamiento matemático de la Antigüedad a nuestros días. Vol.1. Alianza Universidad, n.º 715, Madrid.

1 GONZÁLEZ U., Pedro Miguel. La historia de las matemáticas como recurso didáctico e instrumento para enriquecer culturalmente su enseñanza. Revista SUMA. Febrero, 2004. España. p. 17.

3	¿Cómo crear contextos adecuados para poder enseñar matematizando?...necesitamos problemas matemáticos que tengan un contexto significativo para los estudiantes. Hans Freudenthal.

GUÍA DEL PROFESOR

TEMA: Las matemáticas en la vida cotidiana
Resultados esperados
Al término de la sesión los estudiantes:
Apreciarán que las matemáticas están inmersas en la vida cotidiana y más próxima de las personas.
Aplicarán el pensamiento lógico matemático en la estructura social y laboral de su entorno.

Introducción

Entenderemos por matematización el proceso de trabajar la realidad a través de ideas y conceptos matemáticos, debiéndose realizar dicho trabajo en dos direcciones opuestas: a partir del contexto deben crearse esquemas, formular y visualizar los problemas, descubrir relaciones y regularidades, hallar semejanzas con otros problemas..., y trabajando entonces matemáticamente hallar soluciones y propuestas que necesariamente deben volverse a proyectar en la realidad para analizar su validez y significado.

Siguiendo las ideas del proyecto PISA (Programme for Indicators of Student Achievement), deberíamos prestar atención al desarrollo de grandes competencias y habilidades tales como pensar matemáticamente, saber argumentar, saber representar y comunicar, saber resolver, saber usar técnicas matemáticas e instrumentos...pero también saber modelizar.

Pero no debemos olvidar que el objetivo de enseñar todas estas habilidades debe ser el poder trabajar las grandes ideas tales como: cambio, crecimiento, espacio, forma, azar, dependencia, relaciones, razonamiento cuantitativo, ideas que habrán de delimitar el tipo de instrumentos matemáticos a poner en juego...

El contexto puede ser la vida cotidiana, cultural, científica, artificial, matemático, etcétera. Los problemas del mundo real serán usados para desarrollar conceptos matemáticos... luego habrá ocasión de abstraer, a diferentes niveles, de formalizar y de generalizar... y volver a aplicar lo aprendido y reinventar la matemática.1

Sugerencias didácticas: A través de esta sesión exponga a los alumnos que las matemáticas son mucho más que simples números y formas y que al abordarlas desde una perspectiva cotidiana, es decir, en continuo contacto con las situaciones del mundo real tienen su razón de ser.

Hágalos reflexionar sobre el hecho de que para comprender e interpretar el mundo real en diferentes situaciones y contextos es necesario encontrar una explicación basada en un razonamiento lógico matemático, es decir, buscar una explicación lógica en la vida cotidiana.

Cuestióneles sobre situaciones en las que se hayan enfrentado al hecho de conocer o no algunos planteamientos económicos y los hayan puesto en un dilema para decidir cuál es la mejor opción, y enfatice que por ello es muy importante que desarrollen las habilidades del razonamiento lógico matemático.

ACTIVIDAD 1

Los estudiantes leen y reflexionan sobre el siguiente texto de Javier Peralta2:

Es necesario propiciar la aplicación de las matemáticas a la vida real. Con relación a este aspecto, indudablemente positivo, acaso convenga recordar que sus dos ramas iniciales: aritmética y geometría nacieron para resolver problemas de la vida ordinaria; la primera por la necesidad del empleo de los números para contar y efectuar transacciones comerciales, y la segunda para realizar mediciones...

Como es sabido, en un modelo matemático se pueden considerar tres fases: la abstracción, mediante la cual se procede a definir los conceptos partiendo de la realidad o de ideas intuitivas; el razonamiento lógico matemático con el que se construye la correspondiente teoría, estableciéndose los teoremas y proposiciones; la concreción o proyección de estos resultados al campo real para obtener aplicaciones.

Sin embargo, la enseñanza de la matemática se ha reducido a la segunda, esto es, al razonamiento lógico, desprovisto de toda significación real; y como consecuencia, en la enseñanza se ha producido un divorcio entre las matemáticas y la realidad. Las matemáticas se han presentado entonces imbuidas en un exceso de formalismo, pero sin ninguna utilidad, no teniendo en consideración que se desarrollarán inicialmente, y así transcurrieron a lo largo de los siglos, por dos motivos principales: para satisfacer necesidades sociales o de la vida cotidiana, o como ayuda de otras ciencias, fundamentalmente la física...

La auténtica educación matemática, no obstante, debe fomentar el sentido de aplicación, en su doble vertiente: abstracción y concreción, como asimismo el desarrollo de la intuición...dicho en palabras de Poincaré “es la intuición la que descubre y la lógica la que demuestra”.

Con base en esta lectura, divida al grupo en equipos de trabajo, para que expongan en el siguiente cuadro alguna aplicación de un razonamiento lógico matemático en su entorno más cercano; por ejemplo, si viven en una zona agrícola, cómo es que calculan la cantidad de litros cúbicos que requieren para regar una héctarea, otro ejemplo; si viven cerca de la rivera de un río cómo resolverían en épocas de mucha lluvia que éste no se desborde, etcétera. O bien, si usted conoce alguna problemática y su aplicación matemática, hágaselas saber a manera de ejemplo.

Sugerencia didáctica: Es necesario que les explique y profundice el concepto de Matematización, abordado en la introducción de esta sesión.

Problemática local	Solución intuitiva	Solución lógica matemática

Para concluir esta actividad de trabajo colaborativo en sede, con relación en la competencia del pensamiento lógico matemático, los estudiantes expondrán al grupo los resultados de cada uno de los equipos de trabajo.

ACTIVIDAD 2

Los estudiantes realizarán la lectura: Las Matemáticas Aplicadas a la Vida Cotidiana y otros Lugares Inesperados de Alberto Vargas Mendoza3 que se encuentra en la competencia de Pensamiento lógico-matemático en la Antología del curso. Con base en ella responderán a las siguientes preguntas:

Preguntas:

1.- ¿Crees que las matemáticas te ayudan a resolver problemas de la vida diaria y por qué?

2.- ¿En qué otras áreas del conocimiento el razonamiento lógico matemático tiene una aplicación evidente?

Haga hincapié en que es necesario que completen el siguiente cuadro, lo más detalladamente posible:

Área del conocimiento	Aplicación específica y explicación detallada de ella.

3.-¿Alguna vez habías reflexionado acerca de que el pensamiento lógico matemático pudiera estar tan cerca de tu cotidianidad?

Lecturas complementarias que apoyarán el trabajo:

Definición del Dominio de Competencias Matemáticas de:

PROENZA Garrido, Yolanda, LEYVA Leyva, Luis Manuel, Reflexiones sobre la calidad del aprendizaje y de las competencias matemáticas en: Revista Iberoamericana de Educación, nº 40/6 – 15 de diciembre de 2006, Ed. Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura (OEI), pp 10-12.

Reseña del Premio Nobel de Economía 2007: Ganancias y bienestar social.
En: Sección del Acontecer de Red Escolar, Octubre-Noviembre de 2007. (Disponible en la Antología del curso).

1 ALSINA, Claudi. Si Enrique VIII tuvo 6 esposas, ¿cuántas tuvo Enrique IV?. El realismo en educación matemática y sus implicaciones docentes. En: Revista Iberoamericana de Educación, Enero-Abril 2007, Madrid. No. 43 pp. 91 y 92.

2 PERALTA, Javier. Del análisis de las matemáticas de la L.O.G.S.E. en la Educación Secundaria a otras reflexiones didácticas. En: Tarbiya: revista de investigación e innovación ed., núm. 15 (Enero-Abril,1997) pp. 33-34

3 VARGAS M., Alberto. Matemáticas Aplicadas a la Vida Cotidiana y otros Lugares Inesperados. En: Laberintos e infinitos: Revista de Matemáticos y actuarios del ITAM, No. 7 (Invierno del 2003) pp. 16-20 Disponible en: "http://laberintos.itam.mx/files/179.pdf" http://laberintos.itam.mx/files/179.pdf

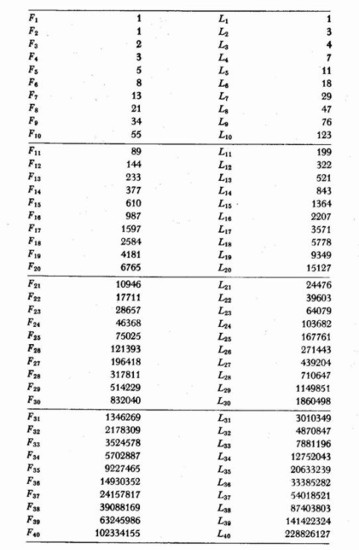
4	Para los pitagóricos, la armonía, uno de los ingredientes de la belleza, va unida al número en la constitución ontológica de todo el universo.

GUÍA DEL PROFESOR

TEMA: Las matemáticas, el arte y la belleza.
Resultados esperados
Al término de la sesión los estudiantes:
Comprender las matemáticas desde una perspectiva del arte y de la belleza y que sus leyes y postulados son los referentes que han utilizado los grandes artistas en sus obras.
Apreciarán que las matemáticas pueden ser producción misma del arte y la belleza.

Introducción

Son muchos los testimonios que confirman la existencia de un verdadero placer estético en la creación y contemplación matemática. Así se expresa H. Poincaré en La Valeur de la Science: "Más allá de la belleza sensible, coloreada y sonora, debida al centelleo de las apariencias, única que el bárbaro conoce, la ciencia nos revela una belleza superior, una belleza inteligible únicamente accesible, diría Platón, 'a los ojos del alma', debida al orden armonioso de las partes, a la correspondencia de las relaciones entre ellas, a la euritmia de las proporciones, a las formas y a los números. El trabajo del científico que descubre las analogías entre dos organismos, las semejanzas entre dos grupos de fenómenos cualitativamente diferentes, el isomorfismo de dos teorías matemáticas es semejante al del artista".1

A través de esta sesión, usted proporcionará elementos a los estudiantes para que identifiquen el placer estético en la contemplación matemática, con una serie de ejemplos que incluyen en los materiales de esta última sesión del bloque.
Es importante que usted les muestre que el mundo de las matemáticas, con el propósito de gozar del objeto bello que se presenta en un teorema, perspectiva, proporción, es necesario crearlo, de tal forma, que este goce estético sea comparable con el de la música, el canto, la danza, la pintura, etcétera.

ACTIVIDAD 1

Los estudiantes consultarán la lectura número 3 denominada El número de oro de Ignacio A. Langarita Felipe que se encuentra en la competencia de Pensamiento lógico-matemático dentro de la Antología del curso y con ella explicarán los siguientes ejemplos de la aplicación de las matemáticas en la belleza y en el arte: la Divina Proporción, la Sección Áurea y la Espiral Logarítmica:

Sugerencia didáctica: Enfatíceles a los estudiantes que sólo revisen los ejemplos concretos que se solicitan en la actividad, ya que la lectura completa del documento la realizarán durante la semana como actividad de estudio independiente.

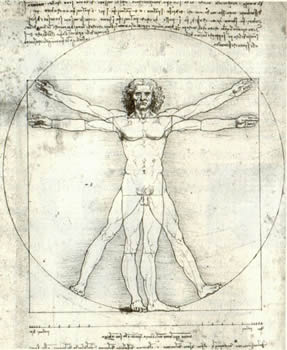	Explicación sobre la proporciones armoniosas del cuerpo humano, que le sirvió a Leonardo Da Vinci para ilustrar la Divina Proporción de Luca Pacioli editada en 1509:
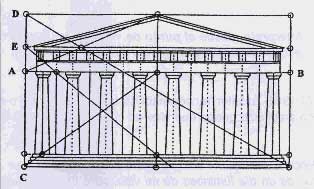	Explicación sobre las proporciones del rectángulo áureo del Partenón:
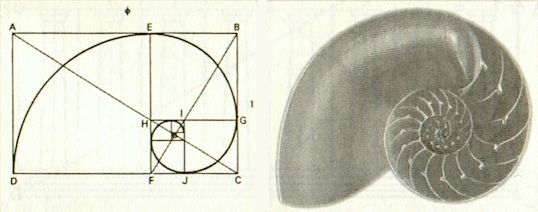	Explicación sobre las proporciones áureas de la espiral logarítimica del Nautilus:

ACTIVIDAD 2

Con base en la lectura completa de: El número de oro de Ignacio A. Langarita Felipe que se encuentra en la competencia de Pensamiento lógico-matemático dentro de la Antología del curso, los alumnos identificarán otros ejemplos relacionados con las proporciones áureas, rectángulos áureos y espirales logarítmicas. Si los estudiantes tienen oportunidad de consultar fuentes alternas pueden incluir otros ejemplos:

Proporción áurea:

Imagen:

Explicación:

Rectángulo áureo:

Imagen:

Explicación:

Espiral logarítmica:

Imagen:

Explicación:

¿DE CIERRE? A MODO DE CONCLUSIÓN DEL TEMA

A través de este bloque hemos expuesto que el pensamiento lógico matemático no es sólo cuestión de números, leyes, teoremas y figuras, es mucho más que todo ello, como bien lo menciona el maestro Miguel De Guzmán:

La matemática es un grande y sofisticado juego que, además, resulta ser al mismo tiempo una obra de arte intelectual, que proporciona una intensa luz en la exploración del universo y tiene grandes repercusiones prácticas. En su aprendizaje se puede utilizar con gran provecho, como hemos visto anteriormente, sus aplicaciones, su historia, las biografías de los matemáticos más interesantes, sus relaciones con la filosofía o con otros aspectos de la mente humana, pero posiblemente ningún otro camino puede transmitir cuál es el espíritu correcto para hacer matemáticas como un juego bien escogido.2

Sugerencia didáctica: Con las actividades desarrolladas hasta el momento y su acompañamiento permanente, esperamos que los estudiantes estén sensibilizados y con una postura más abierta para aprehender e implementar el razonamiento lógico-matemático no sólo en la Universidad sino también en la vida cotidiana.

Por lo que lo invitamos a que los motive en todo momento, que sea pertinente durante la realización del trabajo colaborativo en la sede. Asimismo, le sugerimos que promueva la autoestima y la autopercepción entre los estudiantes, ya que estos aspectos juegan un papel preponderante en el proceso cognitivo de conocimientos y aprendizajes; enfatíceles que es muy importante que ellos se den cuenta de que el éxito de sus aprendizajes es producto de su propio esfuerzo y se perciban como responsables de los conocimientos adquiridos y asuman como propios los objetivos a seguir, que asuman con responsabilidad las metas concretas a lograr en este módulo inductivo y a lo largo de sus estudios universitarios.

Reitere a sus alumnos que el conocimiento y el aprendizaje, no sólo el de las matemáticas, son un fin en sí mismos, para fomentar en ellos el gusto por el conocimiento que rebase los intereses mediatistas.

Por último hágales notar que la autonomía es uno de los objetivos del aprendizaje innovador como el que ellos desempeñarán en esta nueva etapa en la que ellos mismos tendrán que ser los gestores y críticos de su propio conocimiento.

2 DE GUZMÁN, Miguel. Enseñanza de las ciencias y la matemática. En: Revista Iberoamericana de Educación No. 43 – Enero-Abril-2007. Madrid. pp. 45-46

5

La matemática, por su naturaleza misma, es también juego, si bien este juego implica otros aspectos, como el científico, instrumental, filosófico, que juntos hacen de la actividad matemática uno de los verdaderos ejes de nuestra cultura.
Miguel de Guzmán Ozámiz.

TEMA: El papel del juego en la educación matemática

Lectura complementaria que apoyará al profesor para este tema:

DE GUZMÁN Ozámiz, Miguel. Juegos matemáticos en la enseñanza. Publicado en Actas de las IV Jornadas sobre Aprendizaje y Enseñanza de las Matemáticas, Santa Cruz de Tenerife, 10-14 Septiembre de 1984. Sociedad Canaria de Profesores de Matemáticas Isaac Newton.
Disponible en: http://www.sectormatematica.cl/articulos/juegosmaten.pdf

Solución a los ejercicios del Diario Académico del estudiante:

Actividad 1

Actividad 2

11 años

Actividad 3

Un heptágono

Actividad 4

7

4

3

6

2

1

5

Referencias de juegos y actividades lúdicas:

GARDNER, Martin. Números de Fibonacci y de Lucas, Capítulo 13. En libro electrónico: Circo Matemático. Disponible en: http://www.librosmaravillosos.com/circomatematico/capitulo13.html

Educación y Desarrollo, A.C. Calendario Matemático 2008. Disponible en: http://www.educacion.org.mx/index.htm